Exploiting Bitcoin's Merkle Tree Design Flaw in Core Chain's Consensus

Introduction

Earlier this year, I discovered a critical bug in Core Chain - an EVM-compatible blockchain secured by Bitcoin miners. I found the bug in a cryptographic mechanism used to prove how much influence each validator of the chain has. By exploiting it, an attacker can remove the power from all existing validators, compromising the core (pun intended) security assumptions of the chain.

Upon further investigation, I found that the root cause of this bug lies in the original Bitcoin design by Satoshi Nakamoto (and it is actually a known issue).

Note: since finding this bug, Core Chain has made some changes to their design. I will present the system as it was when I did the investigation.

Core Chain

Core Chain is a Proof-of-Stake (PoS) blockchain - it is secured by a set of validators, each with a voting power relative to the amount of their contribution (their stake). Its distinguishing feature compared to other PoS blockchains such as Ethereum, is its consensus mechanism. Specifically, the use of Bitcoin mining power to collect stake in the chain.

Core Chain has two mechanisms for gaining stake in the system:

1. Staking CORE (the native currency of the chain)
2. Mining Bitcoin

We will focus on the second option, and demonstrate how it can be fabricated.

Delegated Proof of Work

Bitcoin miners compete to solve a mathematical puzzle that requires a lot of compute power to solve (computing a small hash for the block header). When a miner finds a valid solution, they can publish a new Bitcoin block, and as a reward, they receive newly minted Bitcoins.

Core Chain uses this mechanism to increase the stake of validators in the chain, by estimating how much work they’ve contributed to Bitcoin. Over time, the fraction of blocks found by a particular miner provides a good approximation of their contributed work. Specifically, the mining power attributed to a validator in Core, is the amount of Bitcoin blocks delegated to this validator by the miners in a certain time period. Miners delegate the block to a Core validator by including its address in the Coinbase transaction, which is always included in the Bitcoin block as the first transaction.

Then, the score (voting power) of each validator is then computed as:

...
    totalPower = 1;
    totalCoin = 1;

    for (uint256 i = 0; i < candidateSize; ++i) {
      Agent storage a = agentsMap[candidates[i]];
      a.power = powers[i] * POWER_BLOCK_FACTOR;
      a.coin = a.totalDeposit;
      totalPower += a.power;
      totalCoin += a.coin;
    }

    scores = new uint256[](candidateSize);
    for (uint256 i = 0; i < candidateSize; ++i) {
      Agent storage a = agentsMap[candidates[i]];
      scores[i] = a.power * totalCoin * powerFactor / 10000 + a.coin * totalPower;
    }
...

Or in short notation: validator_score = validator_mining_power * total_staked_core * power_factor + validator_staked_core * total_mining_power. The key here, is that if all mining powers are zero, no one has any voting power!

BTC light client

But how can Core Chain verify how many Bitcoin blocks are delegated to a specific validator? This is where Simple Payment Verification (SPV) and Merkle proofs come into play, a concept that was introduced in the original Bitcoin whitepaper.

An SPV client stores only Bitcoin’s block headers (containing metadata about the block) instead of all the transactions in the block. Since Bitcoin miners compete to generate the smallest possible hash for the block header, you can verify the validity of a header by simply verifying its hash is small.

Each Bitcoin block header contains a Merkle root, which is a cryptographic summary of all the transactions included in that block. Using a Merkle proof, one can verify that a particular transaction is indeed included in a given block (explained in detail in the following section).

Core Chain uses a light client and a Merkle proof to verify that the transaction delegating the mining power to the validator is included, and extracts the validator’s address from it.

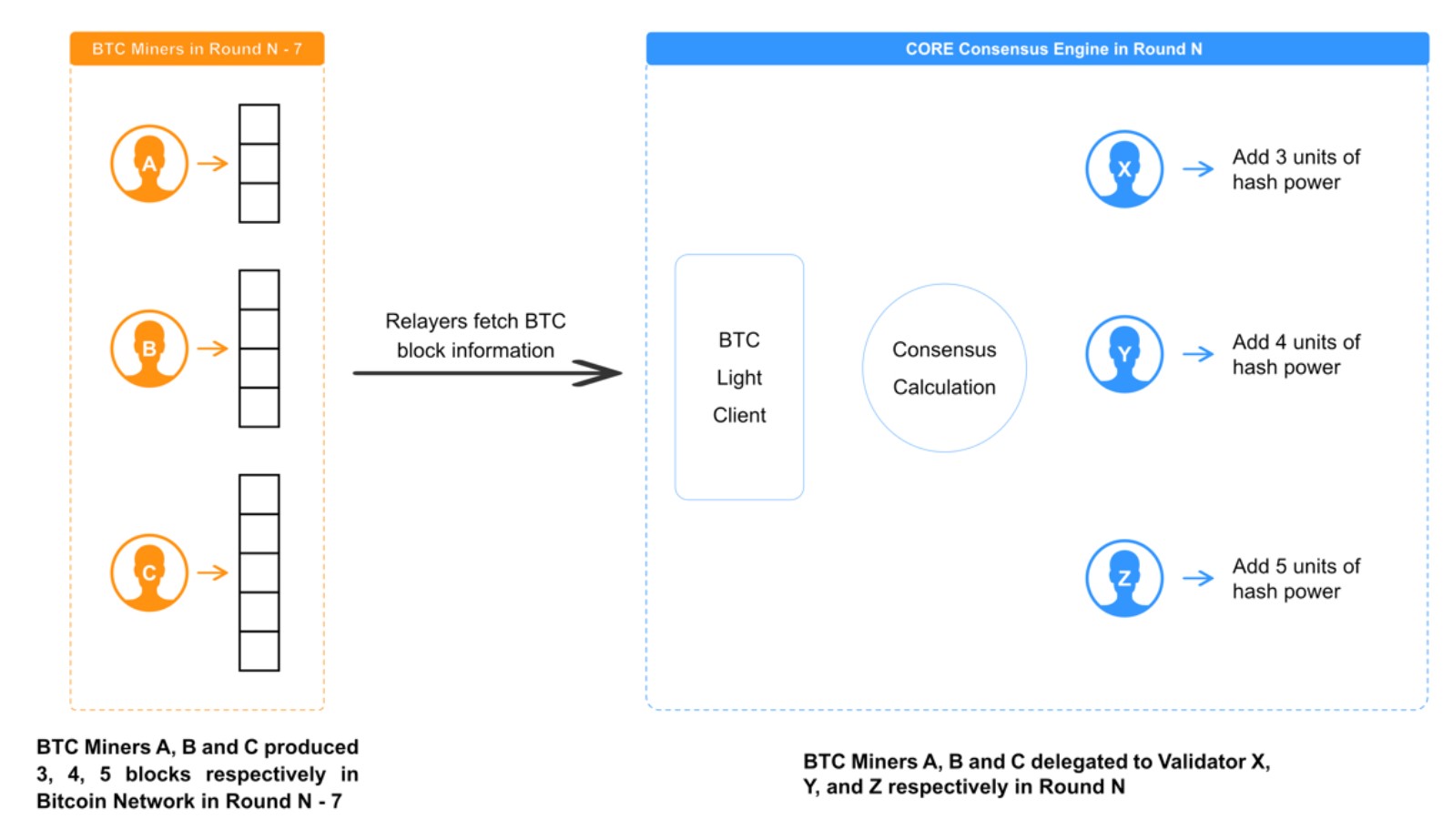Delegated Proof of Work illustration (taken from the Core whitepaper)

Forging a Merkle proof

Using the bug detailed in this section, we can prove that some transaction is included in a Bitcoin block, without it actually being included! However, we don’t have much control over the transaction itself, so the address that is being delegated the mining power is just random. Since a random address does not belong to any real validator, by exploiting this bug the mining power of all validators becomes zero. As we’ve seen in the previous section, this means no validator has any voting power!

Preliminaries

A Merkle tree is a data structure used to commit all the transactions in a block into a single, 32-byte hash called the Merkle root. The Merkle tree is constructed by repeatedly hashing pairs of data until you end up with one final hash. In Bitcoin, the leaves of this Merkle tree represent the hash of individual transactions. Moving up one level, you take two of these transaction hashes, concatenate them, and then hash the result to produce an internal node. You continue this process until there’s only one node left - the Merkle root.

This allows a BTC light client (which has access to the Merkle root) to verify the inclusion of a transaction in a block with using a Merkle proof. The proof contains the transaction itself, and any nodes in the Merkle tree (hashes) that are in the path from the transaction (as a leaf in the tree) to the root.

We illustrate this in the following Merkle tree diagram:

graph TD

    Root["Merkle Root"]
    Root --> B1["H(H(tx1) || H(tx2))"]
    Root --> B2["H(H(tx3) || H(tx4))"]:::highlight
    B1 --> L1["H(tx1)"]
    B1 --> L2["H(tx2)"]:::highlight
    B2 --> L3["H(tx3)"]
    B2 --> L4["H(tx4)"]
    L1 --> T1["tx1"]:::highlight
    L2 --> T2["tx2"]
    L3 --> T3["tx3"]
    L4 --> T4["tx4"]

    classDef highlight fill:#cce5ff,stroke:#0056b3,stroke-width:2px;

The client can then use the highlighted nodes (the Merkle proof) to compute H(tx1), H(H(tx1) || H(tx2)), and finally the root, and compare it to the root in the verified Bitcoin header. If the root is the same, this is a valid proof for the inclusion of tx1.

The bug

The problem with this usage of Merkle proofs is that the same Merkle root is valid for more than one Merkle tree! When internal nodes are transformed into leaves, the Merkle root stays the same, as illustrated here:

graph TD

    Root["Merkle Root"]
    Root --> B1["H(H(tx1) || H(tx2))"]
    Root --> B2["H(H(tx3) || H(tx4))"]:::highlight
    B1 --> L1["H(tx1) || H(tx2)"]:::highlight
    B2 --> L2["H(tx3) || H(tx4)"]

    classDef highlight fill:#cce5ff,stroke:#0056b3,stroke-width:2px;

Using the highlighted nodes, we can prove H(tx1) || H(tx2) is a valid transaction! Usually this is not an issue since the leaves have different structure than internal nodes, but in Bitcoin’s case, there is no mechanism preventing a transaction to be 64 bytes in length, and thus we can exploit this bug to prove inclusion of non-existing transactions!

Exploitation

Only thing left to do, is find how can we include a real transaction in a Bitcoin block, such that concatenating its hash after the hash of the Coinbase transaction will result in a valid 64-byte Coinbase transaction. We can see the structure of the transaction is decoded as follows:

• 4 bytes - version
• Variable size - input count
• List of inputs
  • 32 bytes - Previous output hash
  • 4 bytes - Previous output index
  • Variable size - Coinbase Script length
  • Variable size - Coinbase Script
  • 4 bytes - sequence
• Variable size - output count
• List of outputs
  • 8 bytes - value
  • Variable size - ScriptPubkey length
  • Variable size - ScriptPubKey
• 4 bytes - lock time

How can we use this structure to construct a valid 64-byte transaction, while constraining its contents as little as possible? After a bit of thinking, I found this can be done by only constraining 3 bytes! One can verify that by using a single input (constraining the input count byte to be 1) with Script length of 13 (constraining one more byte), and no outputs (constraining the output count to be 0) - all other bytes can assume any value and we still get a valid 64-byte transaction.

Hence, our constraints on the transaction hashes are as follows: the 5th byte in the first hash should be equal 1, the 10th byte in the second hash should be equal 13, and the 28th byte in the second hash should be equal 0. We can’t control the first hash since it is the Coinbase transaction, but we only have a constraint on one of its bytes, so we will be able to use one out of 256 blocks (about every 2 days). For the second hash, we have 2 bytes of constraints, but we can easily satisfy those if we control the hashed transaction.

Of course, there are more ways to generate 64-byte transactions, and we also have freedom to decide which internal nodes to use in the Merkle tree. Hence, we can significantly increase our chances to successfully exploit the bug.

To fix the bug, Core can simply verify the Coinbase transaction is more than 64 bytes in length, since valid transactions are always longer.

Responsible disclosure

I reported the bug to Core using the Immunefi platform. Immunefi confirmed the bug has Critical severity, but Core responded by saying they don’t consider the exploitation realistic and refused to acknowledge the bug. Not much later, Immunefi removed Core from their bug bounty platform.

I want to emphasize that both Immunefi and Core explicitly approved the publication of this bug, and as far as I know the root cause is still live.

Timeline

• February 19th, 2024: report sent.
• February 21st, 2024: report escalated to Core.
• March 1st, 2024: Core responded, refusing to acknowledge the bug.
• March 19th, 2024: Immunefi confirms the bug is valid and has Critical severity.
• October 16th, 2024: the project and Immunefi approved the publication of the bug.